Contouring

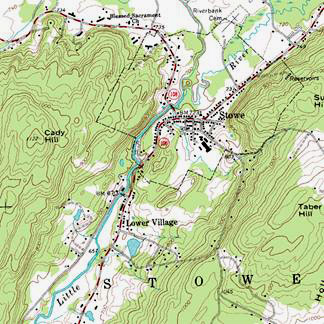
A contour line (also level set, isopleth, isoline, isogram or isarithm) for a function of two variables is a curve connecting points where the function has a same particular value. A contour map is a map illustrated with contour lines, for example a topographic map. The prefix iso-, from the Greek prefix ?s?? ("equal"), is used from descriptive names for map lines that join points of equal value.

Most everyday use of the term is in cartography. A contour map (topographic map) uses contour lines (often just called a "contour") to join points of equal elevation (height) and thus show valleys and hills, and the steepness of slopes.

More generally, a contour line for a function of two variables is a curve connecting points where the function has a same particular value. The prefix iso-, from the Greek prefix ?s?? ("equal"), is used from descriptive names for map lines that join points of equal value. The gradient of the function is always perpendicular to the contour lines. When the lines are close together the length of the gradient is large: the variation is steep. If adjacent contour lines are of the same line width, the direction of the gradient cannot be determined from the contour lines alone. However if contour lines rotate through three or more widths, or if the lines are numerically labelled, then the direction of the gradient can also be determined from the contour lines.

Contour lines are curved or straight lines on a map describing the intersection of a real or hypothetical surface with one or more horizontal planes. The configuration of these contours allows map readers to infer relative gradient of a parameter and estimate that parameter at specific places. Contour lines may be either traced on a visible three-dimensional model of the surface, as when a photogrammetrist viewing a stereo-model plots elevation contours, or interpolated from estimated surface elevations, as when a computer program threads contours through a network of observation points at area centroids.